Phyrs - 0x03

archive time: 2025-07-12

模块与函数的组织是一门技术

• 随时间、位置和速度变化的力
  • 阻尼谐振子
  • 欧拉-克罗默方法
• 求解微分方程
  • 范德波尔振荡器

前面两节大体介绍了动力学的相关概念，并且通过例子说明分析流程

这一节将介绍如何让之前的代码通用

随时间、位置和速度变化的力

之前提到了可以通过欧拉法来分析系统状态变化， 对于一个基本的三维物体，状态可以由质量、位置、速度以及时间来描述：

#[derive(Clone)]
pub struct Particle<R: RealFloat, const E: usize> {
    pub mass: R,
    pub charge: R,
    pub position: VectorC<R, E>,
    pub velocity: VectorC<R, E>,
    pub time: R,
}

此时牛顿第二定律可以表示为：

$$\begin{array}{c}\vec{F}\left(t,\vec{r}(t),\frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}\right)=m\frac{{\mathrm{d}}^2\vec{r}(t)}{\mathrm{d}{t}^2}\\ \\ \frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}=\vec{v}(t),\frac{{\mathrm{d}}^2\vec{r}(t)}{\mathrm{d}{t}^2}=\vec{a}(t)\end{array}$$

此时状态转移方程可以表示为：

$$\begin{array}{c}{\vec{a}}_n=\frac{{\vec{F}}_n\left(t_n,{\vec{r}}_n,{\vec{v}}_n\right)}{m},{\vec{v}}_{n+1}={\vec{v}}_n+{\vec{a}}_n\Delta t\\ \\ {\vec{r}}_{n+1}={\vec{r}}_n+{\vec{v}}_{n+1}\Delta t,t_{n+1}=t_n+\Delta t\end{array}$$

基于这个状态转移方程，我们可以得到一系列的状态：

$$\left(m,{\vec{r}}_0,{\vec{v}}_0,t_0\right)\to \left(m,{\vec{r}}_1,{\vec{v}}_1,t_1\right)\to \cdots \to \left(m,{\vec{r}}_n,{\vec{v}}_n,t_n\right)$$

根据研究的问题判断迭代终止条件，最后的状态就是我们要的结果

使用 Rust 实现可以得到：

impl<'a, R: RealFloat + 'a, const E: usize> Particle<R, E> {
    pub fn default_transition(
        acceleration: Rc<dyn Fn(Self) -> VectorC<R, E>>,
        dt: R,
    ) -> Rc<dyn Fn(Self) -> Self + 'a> {
        Rc::new(move |p: Self| -> Self {
            let velocity = p.velocity.clone() + acceleration(p.clone()) * dt.clone();
            let position = p.position.clone() + velocity.clone() * dt.clone();
            Self {
                mass: p.mass,
                charge: p.charge,
                velocity,
                position,
                time: p.time.clone() + dt.clone(),
            }
        })
    }

    pub fn simulate(self, transition: Rc<dyn Fn(Self) -> Self>) -> Iterate<'a, Self> {
        Iterate::of(transition, self)
    }
}

阻尼谐振子

作为受力随位置和速度相关的例子，可以考虑有一个阻尼谐振子， 即一个竖直悬挂的弹簧，末端有一个小球

假设向上为正方向，并且零点选择在弹簧平衡时的末端位置， 小球质量为 $2.7\mathrm{g}$，半径为 $2\mathrm{cm}$

假设空气阻力系数为 $C=2$，空气密度为 $\rho =1.2kg/{\mathrm{m}}^3$， 重力加速度为 $g={\pi }^{2}m/{\mathrm{s}}^2$，则此时系统受力为：

$$\begin{array}{c}{\vec{F}}_{\text{total}}=\vec{G}+{\vec{F}}_k+\vec{f}\\ \\ \vec{f}=-\frac{1}{2}C\rho A\Vert \vec{v}\Vert \vec{v}\\ \\ \vec{G}=m\vec{g},{\vec{F}}_k=-k\Delta \vec{r}\end{array}$$

其中 $\Delta \vec{r}$ 表示弹簧距离平衡点的相对位移

若劲度系数 $k=0.8kg/{\mathrm{s}}^2$，初始位置为 $10\mathrm{cm}$，初速度为 $\vec{v}=\vec{0}$，则：

use std::rc::Rc;

use phyrs::newton::particle::Particle;
use plotters::{
    chart::ChartBuilder,
    prelude::{BitMapBackend, IntoDrawingArea},
    series::LineSeries,
    style::full_palette::{BLUE_400, YELLOW_50},
};
use rmatrix_ks::{
    matrix::vector::{VectorC, basis_vector},
    number::{
        instances::double::Double,
        traits::{floating::Floating, fractional::Fractional, zero::Zero},
    },
};

fn main() {
    run().unwrap()
}

fn run() -> Option<()> {
    // 初始状态
    let state = Particle::<Double, 1>::without_charge(
        Double::of(2.7e-3),
        VectorC::of(&[0.1].map(Double::of))?,
        VectorC::default(),
        Double::zero(),
    );
    // 加速度
    let total_acc = Rc::new(|s: Particle<Double, 1>| -> VectorC<Double, 1> {
        let g = -basis_vector(1) * Double::PI.power(Double::of(2.0));
        g   // 重力
            - (s.position * Double::of(0.8) // 弹力
            + s.velocity // 空气阻力
                * Double::of(2.0) // 空气阻力系数
                * Double::of(1.2) // 空气密度
                * Double::PI
                * Double::of(2e-2).power(Double::of(2.0)) // A = pi r^2
                * Double::half()) / s.mass
    });
    // 模拟计算
    let one_step = Particle::default_transition(total_acc, Double::of(0.001));
    // 计算 0 到 3 秒内的运动轨迹
    let states = state
        .simulate(one_step)
        .take_while(|s| s.time <= Double::of(3.0));
    // 绘图
    let draw_area = BitMapBackend::new("result/draw_damp.png", (960, 512)).into_drawing_area();
    draw_area.fill(&YELLOW_50).ok()?;
    let mut chart = ChartBuilder::on(&draw_area)
        .margin(10)
        .caption("阻尼谐振子", ("Zhuque Fangsong (technical preview)", 48))
        .x_label_area_size(48)
        .y_label_area_size(64)
        .build_cartesian_2d(0.0..3.0, -0.2..0.2)
        .ok()?;
    chart
        .configure_mesh()
        .axis_desc_style(("Zhuque Fangsong (technical preview)", 24))
        .x_desc("时间 (s)")
        .y_desc("位置 (m)")
        .draw()
        .ok()?;
    chart
        .draw_series(LineSeries::new(
            states.map(|s| (s.time.raw(), s.position[(1, 1)].raw())),
            &BLUE_400,
        ))
        .ok()?;
    draw_area.present().ok()?;

    Some(())
}

得到的图像为：

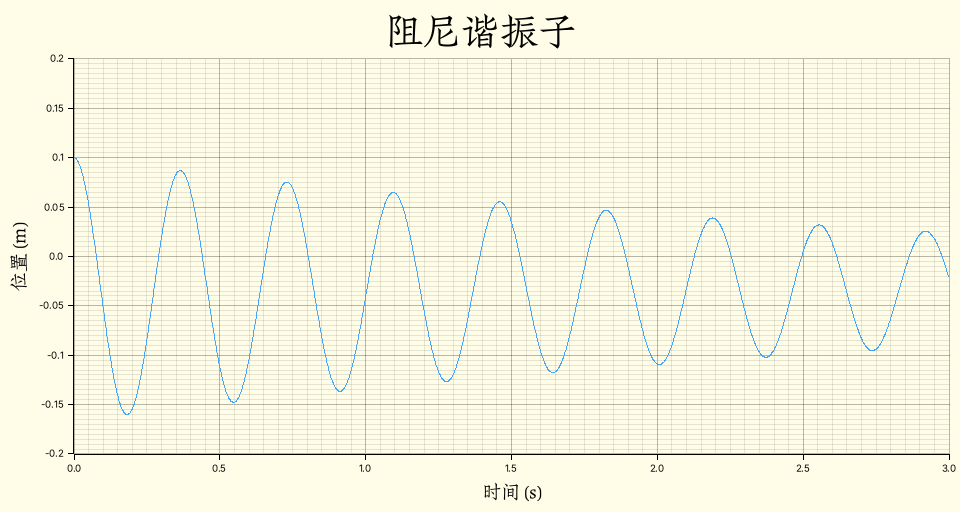
可以看到，由于小球的重力，系统的平衡点并不是最初的 $0\mathrm{m}$， 而是 $z_0=mg/k\approx 0.033\mathrm{m}$

欧拉-克罗默方法

实际上，我们使用的方法是欧拉-克罗默方法¹

通常的欧拉法使用的是上一个状态的速度来计算下一个状态的位移， 而欧拉-克罗默方法则是使用下一个状态的速度来计算下一个状态的位移，即：

$$\{\begin{array}{ll}{\vec{r}}_{n+1}={\vec{r}}_n+{\vec{v}}_n\Delta t& \text{Euler method}\\ & \\ {\vec{r}}_{n+1}={\vec{r}}_n+{\vec{v}}_{n+1}\Delta t& \text{Euler–Cromer}\end{array}$$

欧拉-克罗默方法的结果比欧拉法更符合能量守恒，精度和稳定性也比欧拉法高

求解微分方程

大部分动力学问题都可以转化为一个求解微分方程的问题

但是大部分微分方程很难得到一个精确解，所以求解微分方程更多的还是使用数值方法，例如欧拉法

由于数值方法多种多样，所以在 Particle 中， simulate 接受 transition 而不是合力，这是为了将模拟过程与数值方法解耦

比如我们还可以使用四阶龙格-库塔方法²：

// Self: Particle<R, E>
pub fn general_rk_transition<const K: usize>(
    acceleration: Rc<dyn Fn(Self) -> VectorC<R, E>>,
    dt: R,
    c: VectorC<R, K>,
    a: Matrix<R, K, K>,
    b: VectorC<R, K>,
) -> Rc<dyn Fn(Self) -> Self + 'a> {
    Rc::new(move |p: Self| -> Self {
        // init
        let mut k_dv_dt = vec![VectorC::default(); K + 1];
        let mut k_dr_dt = vec![VectorC::default(); K + 1];
        let mut pk = p.clone();
        k_dv_dt[1] = acceleration(pk.clone());
        k_dr_dt[1] = pk.velocity.clone();
        // iter
        for i in 2..=K {
            let mut ki_dv_dt = VectorC::default();
            let mut ki_dr_dt = VectorC::default();
            for j in 1..i {
                ki_dv_dt = ki_dv_dt + k_dv_dt[j].clone() * a[(i, j)].clone();
                ki_dr_dt = ki_dr_dt + k_dr_dt[j].clone() * a[(i, j)].clone();
            }
            pk = Self {
                position: p.position.clone() + ki_dr_dt * dt.clone(),
                velocity: p.velocity.clone() + ki_dv_dt * dt.clone(),
                time: p.time.clone() + c[(i, 1)].clone() * dt.clone(),
                ..pk
            };
            k_dv_dt[i] = acceleration(pk.clone());
            k_dr_dt[i] = pk.velocity.clone();
        }
        // result
        let position = p.position
            + b.linear_iter()
                .zip(k_dr_dt.iter().skip(1))
                .map(|(bi, dr_dt_i)| dr_dt_i.clone() * bi.clone())
                .fold(VectorC::default(), |acc, e| acc + e)
                * dt.clone();
        let velocity = p.velocity
            + b.linear_iter()
                .zip(k_dv_dt.iter().skip(1))
                .map(|(bi, dv_dt_i)| dv_dt_i.clone() * bi.clone())
                .fold(VectorC::default(), |acc, e| acc + e)
                * dt.clone();

        Self {
            mass: pk.mass,
            charge: pk.charge,
            position,
            velocity,
            time: p.time + dt.clone(),
        }
    })
}

pub fn rk4_transition(
    acceleration: Rc<dyn Fn(Self) -> VectorC<R, E>>,
    dt: R,
) -> Rc<dyn Fn(Self) -> Self + 'a> {
    let one_over_three = R::one() / from_integral(Int::of(3));
    let one_over_six = R::one() / from_integral(Int::of(6));
    let mut c = VectorC::default();
    c[(2, 1)] = R::half();
    c[(3, 1)] = R::half();
    c[(4, 1)] = R::one();
    let mut a = Matrix::default();
    a[(2, 1)] = R::half();
    a[(3, 2)] = R::half();
    a[(4, 3)] = R::one();
    let mut b = VectorC::default();
    b[(1, 1)] = one_over_six.clone();
    b[(2, 1)] = one_over_three.clone();
    b[(3, 1)] = one_over_three;
    b[(4, 1)] = one_over_six;
    Self::general_rk_transition::<4>(acceleration, dt, c, a, b)
}

不过多数情况下，欧拉-克罗默方法的精度就已经足够了

范德波尔振荡器

这里再展示一个求解微分方程的例子，即范德波尔振荡器：

$$\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}-\mu \left(1-x^2\right)\frac{\mathrm{d}x}{\mathrm{d}t}+x=0$$

类比牛顿第二定律，假设质量和劲度系数都为 $1$，此时合力可以看成：

$$\begin{array}{c}{F}_{\text{total}}=F_k+F_{\text{damp}}\\ \\ F_k=-x,F_{\text{damp}}=\mu (1-x^2)v\end{array}$$

则对于 $\mu =0$、$\mu =2$、$\mu =4$ 和 $\mu =6$ 有如下代码：

use std::rc::Rc;

use phyrs::newton::particle::Particle;
use plotters::{
    chart::{ChartBuilder, SeriesLabelPosition},
    prelude::{BitMapBackend, IntoDrawingArea, PathElement},
    series::LineSeries,
    style::{
        Color,
        full_palette::{
            BLUE_400, BLUEGREY_50, BLUEGREY_400, BROWN_800, GREEN_400, RED_400, YELLOW_50,
        },
    },
};
use rmatrix_ks::{
    matrix::vector::{VectorC, basis_vector},
    number::{
        instances::double::Double,
        traits::{floating::Floating, one::One, zero::Zero},
    },
};

fn main() {
    run().unwrap()
}

fn run() -> Option<()> {
    // 初始状态
    let state = Particle::<Double, 1>::without_charge(
        Double::one(),
        VectorC::of(&[Double::of(2.0)])?,
        VectorC::default(),
        Double::zero(),
    );
    // 加速度
    let total_acc = |mu: f64| -> Rc<dyn Fn(Particle<Double, 1>) -> VectorC<Double, 1>> {
        Rc::new(move |s: Particle<Double, 1>| -> VectorC<Double, 1> {
            (basis_vector(1)
                * Double::of(mu)
                * (Double::one() - s.position[(1, 1)].clone().power(Double::of(2.0)))
                * s.velocity[(1, 1)].clone()
                - s.position)
                / s.mass
        })
    };
    // 模拟计算
    let states0 = state
        .clone()
        .simulate(Particle::rk45_transition(
            total_acc(0.0),
            Double::of(0.015625),
        ))
        .take_while(|s| s.time <= Double::of(512.0));
    let states2 = state
        .clone()
        .simulate(Particle::rk45_transition(
            total_acc(2.0),
            Double::of(0.015625),
        ))
        .take_while(|s| s.time <= Double::of(512.0));
    let states4 = state
        .clone()
        .simulate(Particle::rk45_transition(
            total_acc(4.0),
            Double::of(0.015625),
        ))
        .take_while(|s| s.time <= Double::of(512.0));
    let states6 = state
        .simulate(Particle::rk45_transition(
            total_acc(6.0),
            Double::of(0.015625),
        ))
        .take_while(|s| s.time <= Double::of(512.0));
    // 绘图
    let draw_area = BitMapBackend::new("result/draw_vanderpol.png", (960, 512)).into_drawing_area();
    draw_area.fill(&YELLOW_50).ok()?;
    let mut chart = ChartBuilder::on(&draw_area)
        .margin(10)
        .caption(
            "范德波尔振荡器",
            ("Zhuque Fangsong (technical preview)", 48),
        )
        .x_label_area_size(48)
        .y_label_area_size(64)
        .build_cartesian_2d(-2.4..2.4, -10.0..10.0)
        .ok()?;
    chart
        .configure_mesh()
        .axis_desc_style(("Zhuque Fangsong (technical preview)", 24))
        .x_desc("位置")
        .y_desc("速度")
        .draw()
        .ok()?;
    chart
        .draw_series(LineSeries::new(
            states0.map(|s| (s.position[(1, 1)].raw(), s.velocity[(1, 1)].raw())),
            &BLUE_400,
        ))
        .ok()?
        .label("mu = 0")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 32, y)], BLUE_400));

    chart
        .draw_series(LineSeries::new(
            states2.map(|s| (s.position[(1, 1)].raw(), s.velocity[(1, 1)].raw())),
            &RED_400,
        ))
        .ok()?
        .label("mu = 2")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 32, y)], RED_400));

    chart
        .draw_series(LineSeries::new(
            states4.map(|s| (s.position[(1, 1)].raw(), s.velocity[(1, 1)].raw())),
            &GREEN_400,
        ))
        .ok()?
        .label("mu = 4")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 32, y)], GREEN_400));

    chart
        .draw_series(LineSeries::new(
            states6.map(|s| (s.position[(1, 1)].raw(), s.velocity[(1, 1)].raw())),
            &BLUEGREY_400,
        ))
        .ok()?
        .label("mu = 6")
        .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 32, y)], BLUEGREY_400));

    chart
        .configure_series_labels()
        .border_style(BROWN_800)
        .label_font(("Zhuque Fangsong (technical preview)", 16))
        .legend_area_size(48)
        .background_style(BLUEGREY_50.mix(0.8))
        .position(SeriesLabelPosition::UpperLeft)
        .draw()
        .ok()?;

    draw_area.present().ok()?;

    Some(())
}

对应位置和速度的相图如下：

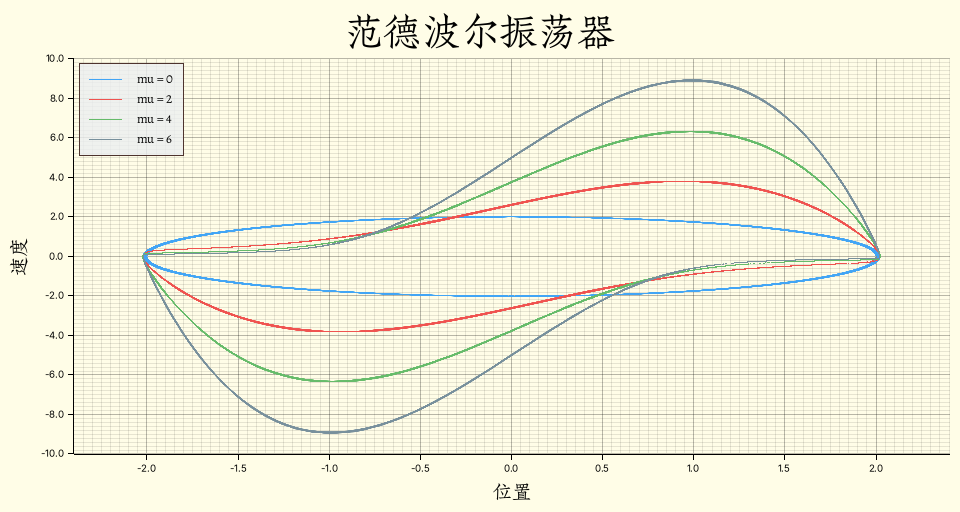
有了龙格-库塔方法，大部分的常微分方程都可以尝试求解了

不过更重要的是知道如何转化物理问题到微分方程，包括如何确定状态转移函数

1. Semi-implicit Euler method.Wikipedia [DB/OL].(2025-04-15)[2025-07-12]. https://en.wikipedia.org/wiki/Semi-implicit_Euler_method ↩

2. Runge–Kutta methods.Wikipedia [DB/OL].(2025-07-07)[2025-07-12]. https://en.wikipedia.org/wiki/Runge–Kutta_methods ↩