Qiskit 线性代数

archive time: 2022-11-08

这个是 IBM 公司 qiskit 文档的线性代数部分的个人翻译

最近毕业论文的课题选定了，量子计算和量子模拟的研究，不过是偏编程实践的，应该还算可做

老师建议使用 qiskit 这个库来实现模拟，所以现在来啃一啃文档，顺便翻译一下

本文是 IBM 公司的 qiskit¹ 工具的文档中，线性代数的内容，原文地址

线性代数

简介

线性代数是表述量子计算的语言，因此，为了能够了解到量子计算中许多惊奇有趣的结构，建立起一个对于包含线性代数在内的基本数学内容的良好认识是至关重要的

这部分的内容目的是建立起一个线性代数的入门基础，使读者能够理解量子计算中的一些过程

希尔伯特空间，正交规范性，以及内积

希尔伯特空间是量子力学和量子计算中最重要的数学结构之一，希尔伯特空间可以被认为是所有量子态组成的态空间

希尔伯特空间与其他矢量空间的主要区别在于，希尔伯特空间支持内积，两个矢量的内积是一个标量

在量子力学和量子计算中，两个态向量的内积表示前一个向量在后一个向量上的投影的长度

而一个向量在某特定方向上的长度表示为在某一特定量子态的概率幅，基于此，不同量子态的观测概率就可以被计算了

对于 $\ket{a}$ 和 $\ket{b}$ ，内积被表示为 $\braket{a | b}$ ，其中 $\bra{a}$ 为 $\ket{a}$ 的共轭转置 $\ket{a}^{\dagger}$ ，即

\braket{a | b} =
  \left(a_1^{\dagger}\ a_2^{\dagger}\ \cdots\ a_n^{\dagger}\right)
  \begin{pmatrix}
    b_1 \\
    b_2 \\
    \vdots \\
    b_n
  \end{pmatrix} =
  a_1^{\dagger} b_1 + a_2^{\dagger} b_2 + \cdots + a_n^{\dagger} b_n

使用希尔伯特空间来表示量子系统，一个最重要的条件是态向量与其自身的内积等于 $1$ ，即 $\braket{\psi | \psi} = 1$

这就是所谓的归一化条件⁴，其物理意义在于，在某一特定态下的量子系统，观测到自身所在态的概率为 $1$

让我们再来看看布洛赫球面

bloch sphere

这个球面连同量子比特态向量之间的内积正是一个希尔伯特空间

并且这个空间还满足归一化条件，因为布洛赫球的半径为 $1$ ，因此每一个向量长度的平方也一定是 $1$

最后关于希尔伯特空间和内积，我们来说说其与酉矩阵的关系

酉矩阵在量子计算中很重要，因为它们对内积进行了保持

也就是说，你使用一系列酉矩阵来变换一个态向量，其归一化条件仍然成立

\braket{\psi|\psi} = 1
    \implies
  \ket{\psi} \to U \ket{\psi} = \ket{\psi^{\prime}} \\
    \implies
  \braket{\psi^{\prime} | \psi^{\prime}}
    = (U \ket{\psi})^{\dagger} U \ket{\psi}
    = \bra{\psi} U^{\dagger} U \ket{\psi}
    = \braket{\psi | \psi} = 1

这表明幺正演化是将一个量子态变为另一个量子态

一个单量子比特的希尔伯特空间使用布洛赫球面来表示，其幺正变换对应旋转某一态向量到球面的其他点，而不影响其长度

外积以及张量积

内积不是唯一的向量乘法，某些情况下，我们会交换 bra 和 ket 的顺序，这也就是所谓的外积

外积的结果是一个矩阵

\ket{b} \bra{a} =
  \begin{pmatrix}
    b_1 \\
    b_2 \\
    \vdots \\
    b_n
  \end{pmatrix}
  (a_1^{\dagger}\ a_2^{\dagger}\ \cdots\ a_n^{\dagger}) =
  \begin{pmatrix}
    b_1 a_1^{\dagger} & b_1 a_2^{\dagger} & \cdots & b_1 a_n^{\dagger} \\
    b_2 a_1^{\dagger} & b_2 a_2^{\dagger} & & \vdots \\
    \vdots & & \ddots & \vdots \\
    b_n a_1^{\dagger} & \cdots & \cdots & b_n a_n^{\dagger}
  \end{pmatrix}

外积使得我们可以使用 bra 和 ket 来表示我们的量子逻辑门而不是使用矩阵

例如 泡利-X 逻辑门 可以表示为 $\ket{0} \bra{1} + \ket{1} \bra{0}$

外积其实是张量积的一个特例

更一般来说，我们会经常看见使用张量积来共享多个量子比特的状态

\ket{a} \otimes \ket{b} = \ket{a \,b} =
  \begin{pmatrix}
      a_1 \ket{b}\\
      a_2 \ket{b}
  \end{pmatrix} =
  \begin{pmatrix}
      a_1 b_1\\
      a_2 b_2\\
      \vdots\\
      a_n b_n
  \end{pmatrix}

而对于矩阵，张量积可以表示为如下形式，更多内容可以参考这里

\mathbf{A} \otimes \mathbf{B} =
  \begin{pmatrix}
      a_{11} \mathbf{B} & \cdots & a_{1n} \mathbf{B}\\
      \vdots & \ddots & \vdots\\
      a_{m1} \mathbf{B} & \cdots & a_{mn} \mathbf{B}
  \end{pmatrix}

特征向量与特征值

让我们来看看下面这个表达式

\mathbf{A} \ket{v} = \lambda \ket{v}

其中 $\mathbf{A}$ 是一个矩阵，而 $\lambda$ 是一个数

如果给定一个矩阵，我们能找到这样一个向量 $\ket{v}$ 和数 $\lambda$ ，那么这个向量被称为特征向量，而这个数被称为特征值

特征值和特征向量在量子力学中有很重要的物理意义，在量子计算中也同样如此

给定矩阵 $\mathbf{A}$ 我们通过等式变换可以得到

\left( \mathbf{A} - \lambda \mathbf{I} \right) \ket{v} = \mathbf{0}

如果 $\mathbf{A} - \lambda \mathbf{I}$ 可逆，那么我们就会得到 $\ket{v} = \mathbf{0}$ ，这是不可能的

所以我们可以有

\det{\left( \mathbf{A} - \lambda \mathbf{I} \right)} = 0

对于 泡利-Z 矩阵，我们可以得到 $\lambda = \pm 1$ ，其中 泡利-Z 矩阵 为

\sigma_z = \begin{pmatrix}
    1 & 0 \\
    0 & -1
  \end{pmatrix}

故对于 $\lambda = 1$ ，特征向量为 $\dbinom{1}{0}$ ，而 $\lambda = -1$ 对应着 $\dbinom{0}{1}$

所以，当我们在 Z 空间 中观测量子比特，我们可以转而观测 泡利-Z 矩阵 的特征向量

事实上，下列属性在量子计算的门模型中是非常重要的，在这里我们处理的是有限维的向量空间

哈密顿矩阵具有线性独立的特征向量，特征向量的数量等于其空间的维数

此外，当相应的特征值不同时，这些特征向量是正交的，当特征值相同时，特征向量不是正交的，但它们仍然是线性独立的，可以被正交化，因此，哈密顿矩阵的特征向量构成了向量空间的一个基础
因为酉矩阵是正规矩阵，酉矩阵的特征向量可以构成一个向量空间的正交基

上面这些特征都可以用泡利矩阵来验证

矩阵幂

矩阵幂的概念是一个非常具体而又极其重要的概念

我们经常看到以下形式的幺正变换

\mathbf{U} = \mathbf{e}^{\mathbf{i} \gamma \mathbf{H}}

其中， $\mathbf{H}$ 是一个哈密顿矩阵， $\gamma$ 是一个实数，易证满足该式所有矩阵都是幺正的

\mathbf{U}^{\dagger} = \mathbf{e}^{- \mathbf{i} \gamma \mathbf{H}^{\dagger}}
  = \mathbf{e}^{- \mathbf{i} \gamma \mathbf{H}}

故 $\mathbf{U} \mathbf{U}^{\dagger} = \mathbf{I}$

你可能会对于这种指数的形式有所顾忌，但是当我们将式子进行 Taylor 展开后，就会明了许多

\mathbf{e}^{\mathbf{i} \gamma \mathbf{H}}
  = \sum_{n = 0}^{\infty}{\dfrac{\left( \mathbf{i} \gamma \mathbf{H} \right)^n}{n!}}

如果我们将 $\mathbf{H}$ 换成 $\mathbf{B}$ ，其中 $\mathbf{B}$ 是对合矩阵，即 $\mathbf{B}^2 = \mathbf{I}$ ，则

\sum_{n = 0}^{\infty}{\dfrac{\left( \mathbf{i} \gamma \mathbf{B} \right)^n}{n!}}
  = \cos{\left( \gamma \right)} \mathbf{I} + \mathbf{i} \sin{\left( \gamma \right)} \mathbf{B}

我们可以将式子分成实部和虚部两个部分

\sum_{n = 0}^{\infty}{\dfrac{\left( \mathbf{i} \gamma \mathbf{B} \right)^n}{n!}}
  = \sum_{n = 0}^{\infty}{\dfrac{(-1)^n \gamma^{2n} \mathbf{B}^{2n}}{\left( 2n \right)!}} +
    \mathbf{i} \sum_{n = 0}^{\infty}{\dfrac{(-1)^n \gamma^{2n + 1} \mathbf{B}^{2n + 1}}{\left( 2n + 1 \right)!}}

由于 $\mathbf{B}^2 = \mathbf{I}$ ，则 $\mathbf{B}^{2n} = \mathbf{I}^n = \mathbf{I}$ ，且 $\mathbf{B}^{2n + 1} = \mathbf{B}$

则证得

\cos{\left( \gamma \right)} \mathbf{I} + \mathbf{i} \sin{\left( \gamma \right)} \mathbf{B} =
  \sum_{n = 0}^{\infty}{\dfrac{(-1)^n \gamma^{2n} \mathbf{B}^{2n}}{\left( 2n \right)!}} +
    \mathbf{i} \sum_{n = 0}^{\infty}{\dfrac{(-1)^n \gamma^{2n + 1} \mathbf{B}^{2n + 1}}{\left( 2n + 1 \right)!}}

注意到，泡利矩阵不仅仅是幺正的，还是哈密顿矩阵，同时也是对合矩阵

这意味着 $\exp{\left( \mathbf{i} \gamma \sigma_k \right)},\ k \in \lbrace x, y, z \rbrace$ 不仅仅可以作为酉矩阵作用在量子态向量上，还可以使用 $\cos$ 和 $\sin$ 的形式来表示，这在量子计算中是十分有用的

如果对于一个矩阵 $\mathbf{M}$ 有特征值 $\lambda$ 以及对应特征向量 $\ket{v}$ ，则

\mathbf{e}^{\mathbf{M}} \ket{v} = \mathbf{e}^{\lambda} \ket{v}

这个也是十分有用的，当我们创建量子电路来模拟某个特定的哈密顿量时，特别是变分电路，我们会经常使用形如 $\exp{\left( \mathbf{i} \gamma \sigma_z \right)}$ 的逻辑门，由于 $\ket{0}$ 和 $\ket{1}$ 是 $\sigma_z$ 的特征向量，所以我们可以断定 $\exp{\left( \mathbf{i} \gamma \sigma_z \right)}$ 在 $\ket{0}$ 有 $\mathbf{e}^{\mathbf{i}\gamma}$ 相，而在 $\ket{1}$ 有 $\mathbf{e}^{-\mathbf{i}\gamma}$ 相

然后，我们可以很轻松的用 CNOT 和 相位/旋转逻辑门 来构建这个逻辑门，因为我们知道这个门在每个计算基态上的数学结果

这里有一些常用量子逻辑门，可以参考

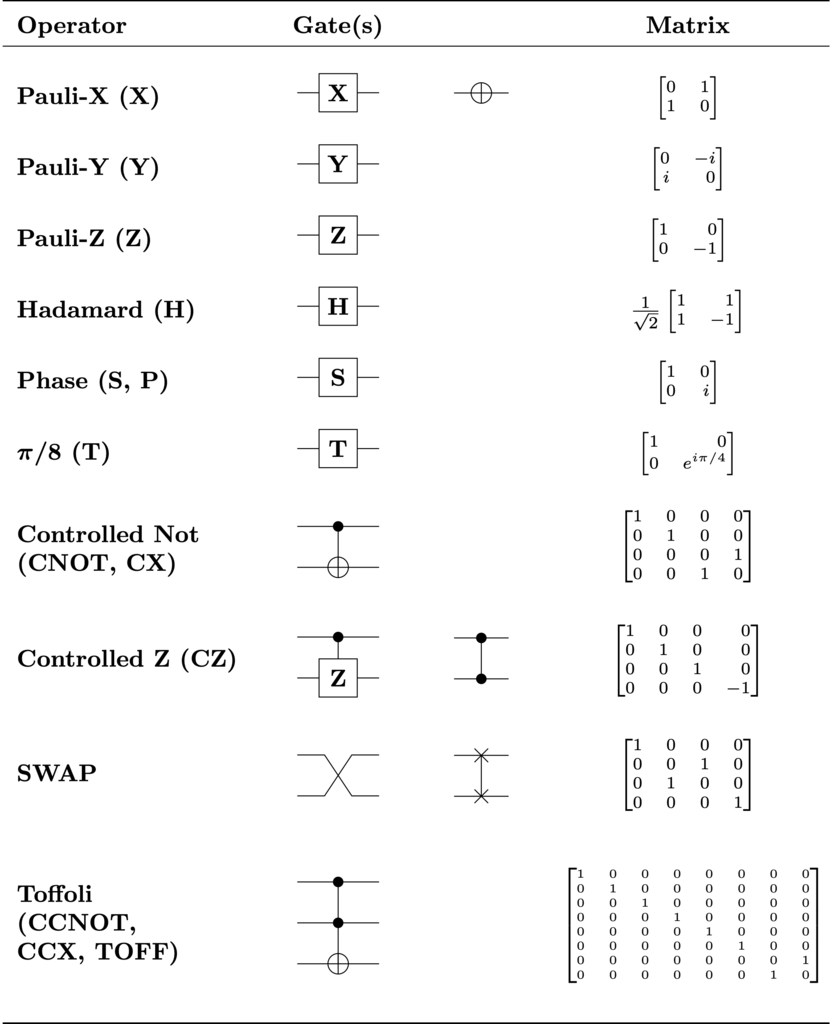
qubit gate

Qiskit: v1.2.0[CP/OL].(2024-08-16)[2022-11-08]. https://github.com/Qiskit/qiskit ↩
线性组合.Wikipedia [DB/OL].(2022-07-01)[2022-11-08]. https://en.wikipedia.org/wiki/Linear_combination ↩
默认情况下，向量都指的是列向量 ↩
Orthonormality.Wikipedia [DB/OL].(2022-11-06)[2022-11-08]. https://en.wikipedia.org/wiki/Orthonormality ↩

Kevin Stephen's Blogs

Qiskit 线性代数

线性代数

简介

向量和向量空间

矩阵和矩阵操作

生成集合，线性相关，基矢量

希尔伯特空间，正交规范性，以及内积

外积以及张量积

特征向量与特征值

矩阵幂

键盘快捷键

Kevin Stephen's Blogs